Hopf Algebren besitzen ein Coradikal, das die Summe aller einfachen Subcoalgebren und damit dual zum (Jacobson-) Radikal ist; insbesondere induziert es eine (Coalgebra-)Filtrierung. Wir nennen sie punktiert, wenn das Coradikal selbst (also der 0. Layer) ein Gruppenring ist; man erhält dann sogar eine Hopf-Algebra-Filtration. Der 1. Layer besteht aus schiefen Ableitungen, welche dann auch höhere Produkte späterer Layer bilden. Generell ist unklar, ob diese bereits die gesamte Hopf Algebra erzeugen (generation in degree 1).
State-of-Art Klassifikation
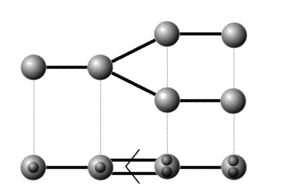
- Eine punktierte Hopf algebra, gelinked aus 4 Borel-Teilen vom Typ A3 [1]
Für den Fall einer abelschen Gruppe gibt es im endlich-dimensionalen ein weitgehendes Klassifikationsresultat von N. Andruskiewitsch und H.-J. Schneider [1] durch verallgemeinerte Dynkin-Diagramme. Es handelt sich um (semidirekte) Radford-Produkte des Gruppenrings und einer Nichols-Algebra; zusätzlich kann über das semidirekte Produkt hinaus ein 2-Cozykel nach G auftreten (Filtrierung dann keine Graduierung), der unzusammenhängende Teile des Diagrams linken kann (siehe rechts).
Nichols Algebren sind die Verallgemeinerung der universellen Einhüllenden für verzopfte Vektorräume, welche in gewissen Fällen endlich-dimensional bleibt. Über abelschen Gruppen existiert dafür eine Klassifikation von I. Heckenberger; sie entsprechen exakt den klassischen Dynkin-Diagrammen, wobei sporadische Fälle für kleine Primzahlen verbleiben [5]. Wesentlich für diese Arbeiten (siehe aber auch unten) sind die generelle Etablierung eines Wurzelsystems; siehe insbesondere die Lecture Notes von Heckenberger.
Im Fall einer nichtabelsche Gruppen konzentriert man sich typischerweise auf die punktierten endlich-dimensionalen Hopf Algebren bzw. Nichols Algebren, die unzerlegbar sind, also im gewissen Sinne die gesamte Gruppe erfordern und so für diese Gruppe "neu" hinzukommen. Es gibt erste Resultate in diesem Fall: Einige explizite Konstruktionen, welche die Coxeter-Struktur der Gruppe ausnutzen (D4, S3, S4, S5 [2]) sowie viele negtive Antworten (höhere An und Sn [3] und die meisten sporadischen einfache Gruppen [4]) indem Teilracks gefunden werden (teilweise mittels GAP) welche bekanntermaßen unendlichen Fällen wie D8 entsprechen (rack of type D) . Bemerkenswerterweise ist auch die endlich-dimensionale Theorie über nichtabelschen Gruppen vollständig einem Wurzelsystem unterworfen [6].
Eigene Resultate
- Eine diagonale E6-Nichols Algebra mit Automorphismus orbifoldet zu einer nichtdiagonalen vom Typ F4 und Konjugationsklassen der Länge 1,1,2,2
Meine Dissertations-Resultate in diesem Gebiet bestehen zum einen aus einer Konstruktion ("Orbifoldizing") solcher Hopf Algebren über zentralen Erweiterungen der Gruppe, sowie in Einzelfällen dem Nachweis (via Gruppen-Cohomologie), dass ein hypothetisches Beispiel über der größeren Gruppe immer auf diese Weise zustandekommt ("De-Orbifoldizing"). Der Ansatz verwendet und produziert natürlicherweise punktierte Hopf Algebren inkl. Liftings!
Die Konstruktion motiviert sich teilweise aus der Quantenfeldtheorie: Zu einer gegebenen Hopf Algebra betrachte man eine Gruppe von Bigalois Objekten (also "twists") und betrachte ähnlich einer Schur-Gruppe ihre direkte Summe; überraschenderweise gibt eine passende Wahl nun wiederum eine neue Hopf Algebra über der erweiterten Gruppe. Dies liefert insbesondere neue Beispiele über Q8, GL(2,3) sowie mit erstaunlich großem Wurzelgitter wie F4 über Z2xZ2xD4 aus einem abelschen E6 Fall:
Für Destruktion und/oder Klassifikation aller Nichols Algebren über der größeren Gruppe ist eine Umkehrung nützlich: Die Anzahl der Möglichen Wirkungen der ("neuen") zentralen Elemente auf dem Yetter-Drinfel'd-Modul ist überschaubar und durch strukturelle Resultate von [6] weiter eingeschränkt. Orbifoldizings sind hier exakt (!) die trivialen, allerdings erzeugen Doi-Twists sofort weitere Möglichkeiten. Im Einzelfall muss dann per Cohomologie geklärt werden, ob letztere Erstere ausschöpfen? Als später relevante Beispiele schließt dieses Argument etwa Faserprodukte von D4 und Q8 der Ordnung 32 aus.
Literatur
[2] A. Milinski, H.-J. Schneider: Pointed indecomposable Hopf algebras over
Coxeter groups, Contemp Math. 267, 215-236, 2000.
[5] Heckenberger: Nichols algebras of diagonal type and arithmetic root systems, Habilitation thesis 2005.
[6] Heckenberger, Schneider: Root system and Weyl gruppoid for Nichols algebras, 2008.